
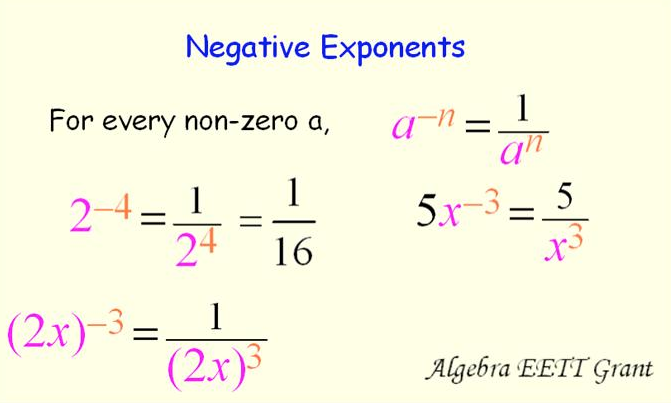
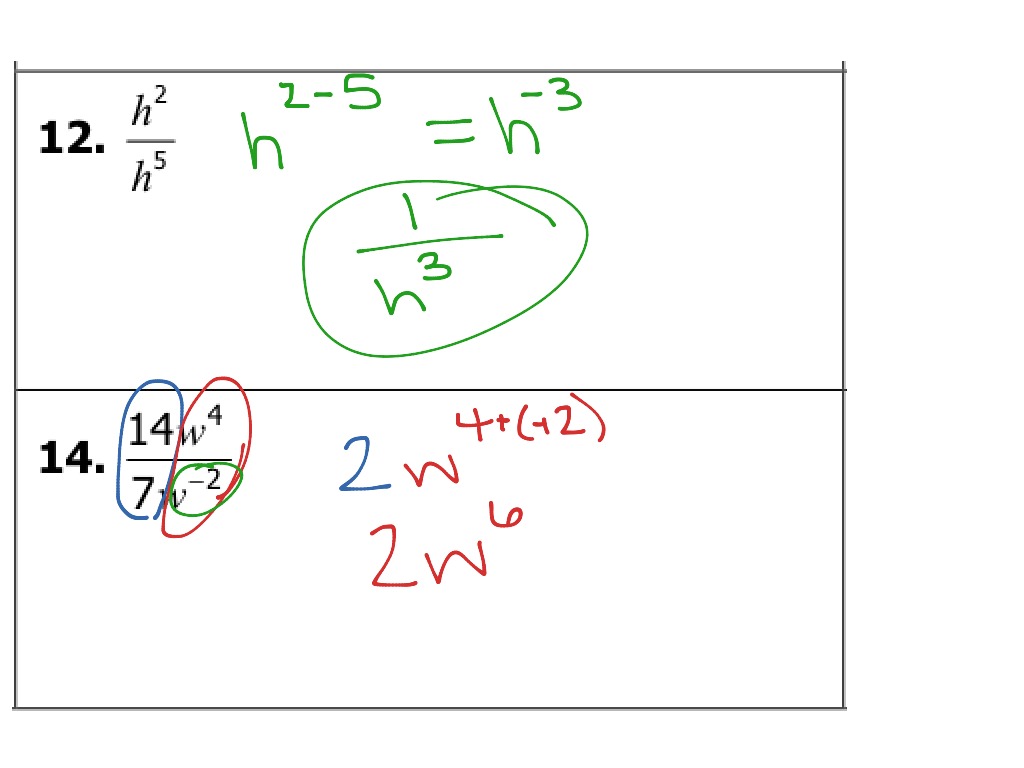
Invert the base to change a negative exponent into a positive.Īny non-zero number raised to the zeroth power is 1. To raise a number with an exponent to a power, multiply the exponent times the power. To find the quotient of two numbers with the same base, subtract the exponent of theĭenominator from the exponent of the numerator. To find the product of two numbers with the same base, add the exponents. Zero Exponent Rule: x 0 = 1, for all x ≠ 0. If we apply the Quotient Rule, we get x 3–5 = x –2.Īgain, it goes back to the Quotient Rule: Find x 3/x 3. In the case of the 12s, you subtract -7- (-5), so two negatives in a row create a positive answer which is where the +5 comes from. What happens when n is > m? You get a negative exponent. The rule for dividing same bases is xa/xbx (a-b), so with dividing same bases you subtract the exponents. Remember the Quotient Rule: x m / x n = x m-n. The Power Rule for Exponents: (a m) n = a m*n. So we have a shortcut (Rule) to find our power: Now use the exponent definition to expand according to the exponent. via GIPHY Step Three: Trash the Negative Sign and Move the Value to the Denominator The final step is to simplify rewriting 5 squared as 25 and concluding that 5-2 is equal to 1/25 or 0.04. For any real number a a and any numbers m m and n n, the power rule for exponents is the following: (22)3 (2 2)3 (2 2) (2 2) (2 2) 26 Use the exponent definition to expand the expression inside the parentheses. We can multiply the exponent by the power to simplify, Definition: The Power Rule For Exponents. Now apply the product rule: x 3+3+3+3 = x 12. Exponent rules are a set of mathematical rules that simplify calculations involving exponents, which are used to indicate how many times a number is multiplied. The Quotient Rule for Exponents: a m / a n = a m–n.Įxpand to (x 3)*(x 3)*(x 3)*(x 3). We also notice that 7 – 4 = 3, which is our shortcut (Rule) to find our quotient. On top over a 1 on the bottom:, which simplifies to or x 3.
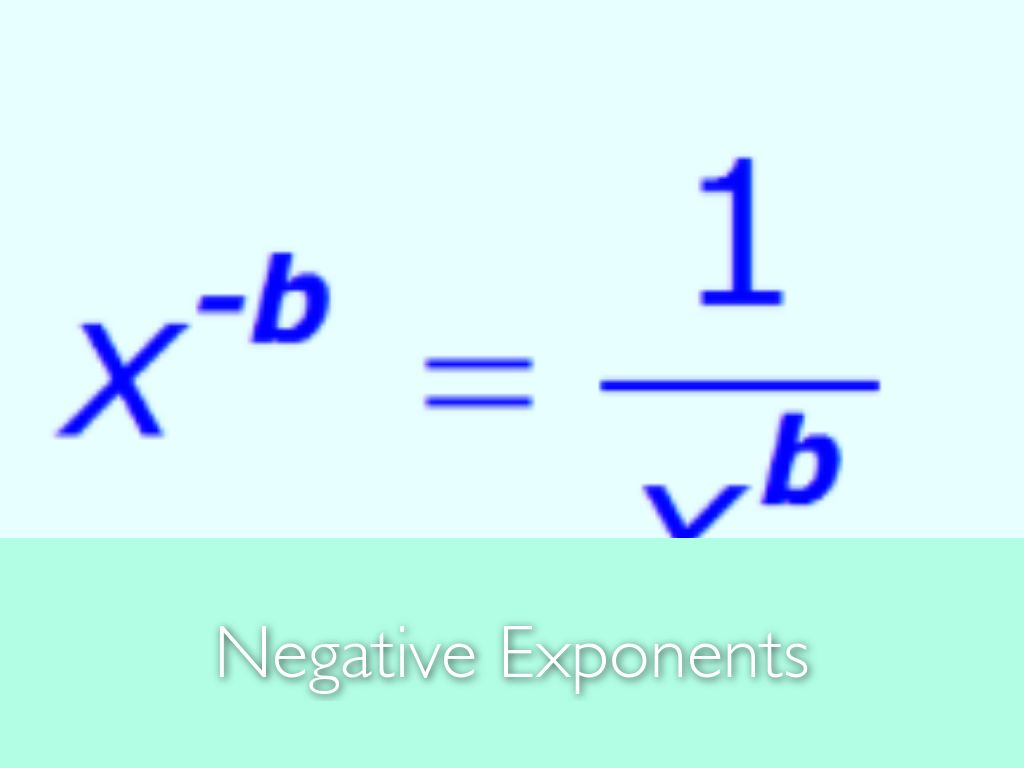
One x in the numerator (on the top) will divide to 1 with one of the x’s in tehĭenominator (on the bottom) until there are no more x’s on the bottom, leaving 3 x’s The Product Rule for Exponents: a m * a n = a m + n.Įxpand to x*x*x*x*x*x*x/ x*x*x*x. When we multiply two numbers having the same base, we can add the original exponents The derivate of 2x is ln (2)2x, which you would solve by applying the Derivative of Exponential Rule: The derivative of an exponential function with. 2x is an exponential function not a polynomial. All the terms in polynomials are raised to integers. Since x is still our base and our new exponent is 8 we can write our product as The Power Rule is for taking the derivatives of polynomials, i.e.
A factor with a negative exponent becomes the same factor. Where did the 8 come from? Well, we have 3 factors of x for the x 3 and 5 factors of x for x 5, and that adds to 8 factors of x. This is true for any nonzero real number, or any variable representing a nonzero real number. Since there are now 8 factors of x, we write x 8. From this, it follows that any power of a number is the. We could expand to (x*x*x) * (x*x*x*x*x), then count the factors of x and convertīack to exponent form. When the exponent is negative, it tells us how many times the base is used in a repeated division of 1. Have developed shortcuts, called RULES, to make the calculations quicker and easier When we calculate using numbers in exponent form that have the same base, we can alwaysĬonvert to expanded form, count the number of factors, then change back to exponentįorm, especially when the base is a variable. For example:ĥ 3 (read five to the third power) means we have 3 factors of 5, or 5*5*5 which simplifiesġ25 is the product or simplified form. This expression means we use b as the factor and we have n factors of b. In the expression b n, b is the base and n is the exponent. An exponent means that we are dealing with products and multiplication. The base is the repeated factor (the number multiplied) and the exponent counts the The number is called the base and the power is given by the exponent. \) miles.A number raised to a power represents a product where the same number is used as a


 0 kommentar(er)
0 kommentar(er)
